Earlier this year I finished hammering out a second Master’s degree, this time from the University of Oklahoma. I specialized in Reference Librarianship (helping people find things) and Information Literacy (teaching skills for information retrieval and evaluation). Many people don’t realize it, but critical thinking and even logic play an important role in the task of information evaluation, especially within digital contexts. In this article I will be focusing on the latter, and explaining about the role logic plays when evaluating online data.
One of the basic principles of logic is that an argument can be wrong in the following four ways:
- there can be false premises,
- there can be true premises that nevertheless do not support the conclusion,
- there can be equivocation of terms,
- there can be a combination of any of the above three things that render the argument unsound.
Consider how this might apply to the following syllogism:
- All Men Are Mortal
- Socrates is a Man
- Therefore, Socrates is Mortal
We can say that the above argument is valid when the conclusion follows logically from the premises. That is to say, if the premises are true then the conclusion necessarily follows. But are the premises actually true? In the case of the above argument, both the premises are true: all men are indeed mortal, and Socrates was indeed a man. It is possible, however, to make an argument that is structurally valid (that is, where the conclusion follows from the premises) but the premises are still false. Here would be an example:
- All Men Are Trees
- Socrates is a Man
- Therefore, Socrates is a Tree
Notice that the conclusion follows logically from the premises even though the premises are false. In order for an argument to work, it must be valid as well as containing true premises. When an argument is both valid and true, and contains no ambiguous terms, then we say the argument is sound.
An example of an argument with ambiguous terms would be the following:
- Only man is a rational animal.
- No woman is a man.
- Therefore, no woman is a rational animal.
This argument has ambiguous terms, because the term “man” is being used in a different sense in premise one and premise two. Thus, even if it is valid, it is not sound, because it doesn’t satisfy the criteria of having no ambiguous terms.
Most of the informal arguments we construct in our day to day lives, or even more formal arguments we might make when writing or having intellectual conversations, do not follow the same strict structure as the above syllogisms. In normal everyday discussions, both the premises and conclusion are sometimes implied, and there are usually many more premises and terms than what we find in a simple syllogism. Even so, all proper arguments are made up of conclusions and premises that purport to support those conclusions. And again, if the premises are true and if the conclusion follows logically from those premises and there are no ambiguous terms, then the argument is sound.
Keep this in mind when you are evaluating sources from the internet. The presence of routine logical errors, like spelling mistakes, can be a give-away that this is a source that may need a higher level of external corroboration before it can be trusted. At the same time, learn to distinguish logical flaws in a source from factual flaws. Just as the presence of a spelling-mistake does not render the sentence false, so the presence of unsoundness in an argument does not necessarily render false all the premises of which that argument consists. A discerning internet-user is able to glean information from the premises of an argument even while disputing the conclusion the author is drawing from that information.
Whenever I read something online, I immediately put on my “logic hat” and go through a mental checklist with the following questions:
- Is the writer’s reasoning sound?
- Does this writer’s conclusions follow logically from the information (premises) he or she has presented?
- If this writer’s information is false, then does that render his conclusion faulty, or can each of these be considered separately?
- What information might still be true even if the author’s conclusions do not follow from the preceding premises?
Many researchers go wrong for failing to ask these types of questions. Even professionals who should be seasoned researchers (for example, journalists, politicians, and even some university professors), find it hard to ask these types of questions about a source. In my experience, people struggle over the fourth question the most, being quick to dismiss information someone presents if the person’s conclusions (or even “where they’re coming from”) is suspect. But a writer’s conclusions might be false while the information they present could still be correct; similarly, a writer’s information could be false while the conclusions they draw from that information could still be correct. And remember, if an argument is sound (that is, if the conclusion really does follow from the premises without any ambiguous terms), then the argument remains sound even if you disagree with the motives or agenda of the person making the argument. (In fact, dismissing an argument because you disagree with the person’s motives is a logical fallacy known as the Ad Hominem fallacy.) Similarly, if information given in a premise is correct, then that information remains correct even if the conclusion that someone draws from that information is unsound, and even if you disagree with the person’s motives who is making the argument.
Let’s make this practical. Leading up to the Senate’s impeachment trial of President Trump in 2019, I was concerned to see leading Republicans making comments like, “I’m not trying to pretend to be a fair juror here,” and adding that they did not intend to offer an unbiased examination of the evidence. Instead, these Republicans acknowledged that they had already made up their mind. Around this time, I made a Facebook post in which I cited the pre-trial oath senators would have to swear promising to do impartial justice, followed by an article from The Atlantic which discussed the implications of Senators taking this oath after conceding that they did not intend to be fair jurors.
This post invited a feeding frenzy from well-meaning conservative friends who wanted to enlighten me on how terrible the Democrats were being, or to explain how there had been no collusion with the Russians, and to explain how the article from The Atlantic was just more of the same “orange-man-bad” bias. Had these friends been trained in logic, they could have avoided the ad hominem, making a differentiation between the real or imagined motives and biases in the Atlantic article, on the one hand, and the more circumscribed constitutional points being made, on the other. Because remember, if an argument is sound (that is, if the conclusion really does follow from the premises without any ambiguous terms, and the premises are all true), then the argument remains sound even if you disagree with the motives or agenda of the person making the argument. Similarly, if information given in a premise is correct, then that information remains correct even if the conclusion that someone draws from that information is unsound, and even if you disagree with the motives of the person making the argument.
Logic also helps us when we evaluate sources in the aggregate and compare for consistency. A good researcher does not simply evaluate a single source in isolation but will compare multiple sources, exposing himself to a variety of viewpoints. He will want to ask not simply “Is this source logical?” but “is this source logically consistent with other reliable sources?”
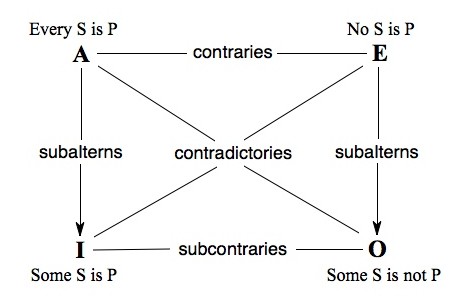
Logic shows us that there are a variety of ways that things can be consistent or inconsistent. On the level of simple statements (i.e. all men are mortal, no men are mortal, some men are mortal, some men are not mortal) there are roughly four ways that statements can be related. These are represented by the Square of Opposition below.
Statements in the top left-hand corner of the Square of Opposition are what we call Universal Affirmative Statements, and these are designated by the letter A. In the top right-hand corner of the Square of Opposition are what we call Universal Negative statements, and these are designated by the letter E. Statements in the bottom left-hand corner of the Square of Opposition are what we call Particular Affirmative statements, and these are designated by the letter I. In the bottom right-hand corner of the Square of Opposition are what we call Particular Negative statements, designated by the letter O.
The relationship between contraries (A and E statements) on the top horizontal axis is such that both statements cannot be true at the same time, although both may be false at the same time. For example, although the statement “all men are mortal” and “no men are mortal” could both be false at the same time (as would be the case in certain Greek myths where only some men are mortal), they cannot both be true at the same time. We describe this relationship between A statements and E statements by saying that they are contraries .
On the other hand, the relationship between subcontrary statements (I and O statements) on the bottom horizontal axis is such that both cannot be false at the same time, although both can be true at the same time. For example, although the I statement “some birds are flying things” could not be false if it is also false that “some birds are not flying things” (because the falsity of “some birds are flying things” must necessarily mean that “some birds are not flying things”), they could both be true at the same time. That is, it could be true that some birds are flying things at the same time as it is also true that some birds (i.e., ostriches) are not flying things.
The diagonal axis (from A to O, and from I to E) represents a contradictory relationship between statements, so that the truth of A implies the falsity of O, and the falsity of A implies the truth of O, and the truth of I implies the falsity of E, while the falsity of E implies the truth of I. For example, the A statement that all fruits contain seeds contradicts the O statement that some fruits do not contain seeds, for if it is true that all fruits contain seeds then it must necessarily be false that some fruits do not contain seeds, but if it is false that all fruits contain seeds then it must necessarily be true that some fruits do not contain seeds.
The vertical axes represent the flow of truth or falsity from A to I and from E to O. If the A statement that every dog is a mammal is true, then this truth flows to position I on the Square of Opposition, meaning that it must also be true that some dogs are mammals. Similarly, if it is true that no reptiles are birds, then it has to also be true that some reptiles are not birds.
These relationships can be summarized as follows, which I grabbed off the Stanford Encyclopedia of Philosophy with minimal modification:
- Two propositions are contraries if they cannot both be true but can both be false.
- Two propositions are subcontraries if they cannot both be false but can both be true.
- Two propositions are contradictory if they cannot both be true and they cannot both be false.
- A proposition is a subaltern of another if it must be true if its superaltern is true, and the superaltern must be false if the subaltern is false.
The square of opposition represents fixed and immutable laws regulating degrees of consistency and inconsistency among statements. It gives you an immediate bunk-detector that you can use when you are online. It does not tell you which statements are true, but how the truth or falsity of different statements relate to each other.
Most of what we read is not written in simple A, E, I, and O statements. This means that in most of the everyday situations we face, including questions about source evaluation, it will be less clear what statements are consistent and inconsistent. In most everyday contexts, what is consistent and inconsistent will follow from empirical observation and probabilities, not from logical laws. And even when we are dealing with straightforward A, E, I, and O statements in everyday life, we must enter into the realm of empirical observation, or perhaps appeal to authority, to find out if the statements are actually true. This is where we rely less on pure logic and more on what is called critical thinking. Yet logic prepares us for critical thinking like playing scales prepares us for playing Chopin.
Consider the following statement. “The allegations concerning Daniel’s adultery must be false because Daniel is a pious Christian who loves his wife.” This argument makes appeal to a criterion of consistency, claiming that the statement “Daniel committed adultery” is inconsistent with our body of knowledge regarding who we know Daniel to be. These are not simple A, E, I, or O statements that can be checked against logical laws, and even if we could reduce this problem to the four types of statements, this would not get us any closer to knowing which statements are true concerning Daniel. Rather, to check into this argument, you would need to explore empirical details, to learn about Daniel’s life, to find out why the allegations have been made, and maybe even listen to your intuition. Yet we are still checking for consistency in a similar way to the Square of Opposition, for we want to know what can be affirmed or denied about Daniel at the same time. What type of statements can be true at the same time? For example, can the statement “Daniel committed adultery” and “Daniel is pious” both be true at the same time? What statements can be false at the same time? For example, could it false that Daniel committed adultery and also false that he is pious? What statements contradict each other? For example, does the truth of Daniel’s piety imply the falsity of the charges against him, or visa versa? Law courts must engage in these types of problems all the time, and these are also problems that we engage in when we conduct source evaluation.
Logic prepares us for these types of real-life situations, just like basic drawing exercises prepares the student for painting. That is why, if I am teaching a student to engage in source evaluation on the internet, one of the first things we would do is spend a few days, or even weeks, running through exercises on the Square of Opposition. I want the student to be able to explain the relationship between contraries, contradictions, subcontraries, and subalterns in his or her sleep before I ever think about turning him or her loose on the internet. Then, when the student does begin evaluating sources, he or she will begin instinctively asking questions about consistency, especially when considering multiple sources in the aggregate as required by Tools #2 and 3. Although it is rare when you can use the Square of Opposition to check consistency within a single internet source, or consistency between multiple sources (because remember, most arguments cannot easily reduce to the four types of statements), nevertheless the student who has performed multiple exercises using the Square of Opposition will be trained to ask the right types of questions of sources. Instinctively, the student will want to know what information can be true or false at the same time, what information contradicts other information, and so forth.
This concern for consistency is a key part of growing in wisdom, and logic prepares the Christian student for wisdom in much the same way that English grammar prepares the student for composing verse. Commenting on the teaching of Proverbs that truth is marked by consistent witness, Dr. Alastair Roberts made the following observation:
“The wise are concerned to demonstrate consistency in their viewpoints, as agreement between witnesses and viewpoints are evidence of the truth of a matter or case. However, the beliefs of a fool are generally marked by great inconsistency. They lack the hallmarks of truth because they are adopted for their usefulness in confirming the fool in his ways, rather than for their truth. The fool will jump between inconsistent positions as a matter of convenience. The consistency of the positions and beliefs of fools are found, not in the agreement of their substance, but in the fact that they all, in some way or another, further entrench the fools in their prior ways and beliefs. Also, the intellectual laziness of fools means that they will not diligently seek to grow in a true consistency (although some might develop a consistency in falsehoods designed merely to inure them against challenge, rather than as a pursuit of truth itself).” From ‘Wisdom and Folly in Christian Responses to Coronavirus.’
During the COVID controversies of 2020, I was involved in a situation that showed me just how important this logical foundation to source evaluation is. Many of my friends were inclined towards various conspiracy theories about COVID-19, and they would sometimes send me sources from the internet for my feedback. One friend, whom I will call Bob, sent me a message on Monday claiming that the pandemic originated as a Chinese bioweapon, but by Monday afternoon he had sent me a YouTube video claiming that the pandemic was engineered by Bill Gates so he could profit on sale of a vaccine. On Wednesday morning, I had another message in my inbox from Bob, in which he shared a source claiming that the coronavirus was a hoax because COVID-19 hospitals were actually empty. Because I cut my teeth analyzing the relationships between statements on the Square of Opposition, it was second nature to me to ask whether these sources (all of which Bob presumably believed to be reliable or he wouldn’t have sent them) could all be true at the same time, and how they were or were not consistent with each other.
“I’m curious,” I wrote to Bob, “how all these sources you’re sending me can all be true at the same time? How can the coronavirus be a deadly weapon from China as well as something Bill Gates invented as well as a hoax that doesn’t actually exist? Essentially, you are asking me to believe that Bill Gates manufactured a virus that originated in China that doesn’t actually exist. That isn’t logical!”
Bob is not an anomaly. Many people like him have ideological reasons for doubting the mainstream media, and this will lead them frequently to latch onto competing explanations with no thought of consistency. For example, one minute they will be disputing the role of experts in mediating knowledge to us, only to turn around and promote an expert (whether Jordan Peterson or John Ioannidis) when it happens to suit their political agenda. For these types of unscrupulous informational charlatans, truth doesn’t matter, which is why they are quite happy to simultaneously share inconsistent theories as long as it furthers their agenda of disrupting people’s confidence in the mainstream.
(By the way, for friends reading this and wondering about the identity of Bob, rest assured that he is not you. He is not anyone because he is a composite drawn from numerous interactions. But in another sense, Bob is all of us – the archetype of what we would all be online but for the grace of God.)
Further Reading
- “Immune to Evidence”: How Dangerous Coronavirus Conspiracies Spread
- A Classical School’s Guide to Senior Thesis Research, Part 2: How to Leverage The Power of Google
- A Classical School’s Guide to Senior Thesis Research, Part 1: How to Find Information Online
- A Classical School’s Guide to Senior Thesis Research, Introduction: Classical Education and Information Literacy
- Classical Education Archives